Khối chóp là một trong những kiến thức quan trọng của khối lớp 12, nếu các bạn không nắm vững được định nghĩa, tính chất và công thức tính thể tích khối chóp sẽ không giải bài tập được. Trong bài viết dưới đây, chúng tôi sẽ trình bày chi tiết từ A – Z để các bạn cùng tham khảo nhé
Định nghĩa khối chóp là gì?
Trong hình học, một hình chóp là một khối đa diện được hình thành bằng cách kết nối một điểm của một đa giác và một điểm, được gọi là đỉnh. Mỗi cạnh cơ sở và đỉnh tạo thành một hình tam giác, được gọi là mặt bên. Một hình chóp với một n cơ sở -sided có n + 1 đỉnh, n + 1 mặt, và 2 n cạnh.
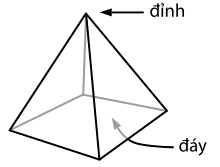
Tính chất của hình chóp
Đường thẳng đi qua một đỉnh và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp.
Tên gọi của hình chóp dựa vào đa giác mặt đáy: hình chóp có đáy là tam giác được gọi là hình chóp tam giác, hình chóp có đáy là tứ giác gọi là hình chóp tứ giác.
Nếu hình chóp có cạnh bên hợp với mặt đáy các góc bằng nhau hoặc các cạnh bên bằng nhau thì chân đường cao chính là tâm đường tròn ngoại tiếp đáy.
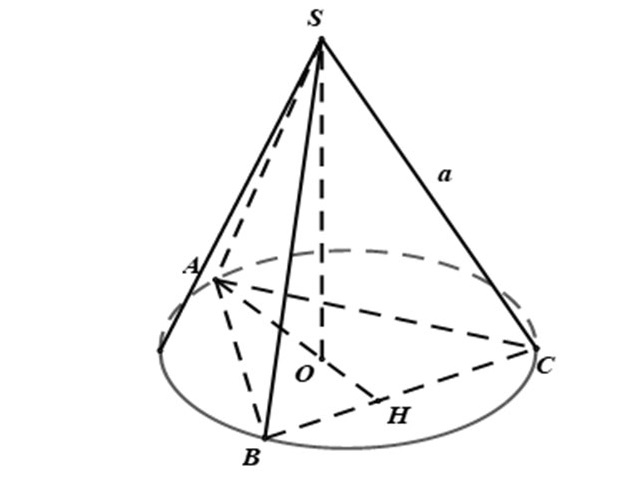
Nếu hình chóp có các mặt bên hợp với mặt đáy các góc bằng nhau hoặc có các đường cao của các mặt bên xuất phát từ 1 đỉnh bằng nhau thì chân đường cao là tâm đường tròn nội tiếp mặt đáy.
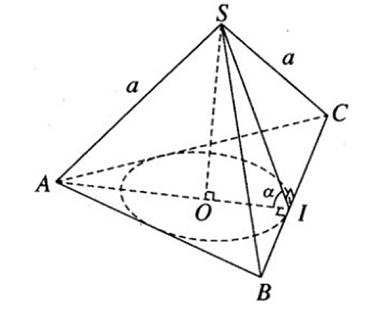
Nếu hình chóp có mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy thì đường cao của hình chóp sẽ là đường cao của mặt bên hoặc mặt chéo đó.
Công thức tính thể tích khối chóp
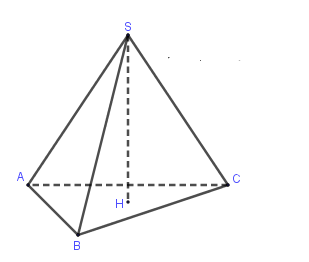
Thể tích hình chóp bằng ⅓ diện tích đáy nhân với chiều cao.
V = ⅓ Sđáy x h
Trong đó:
- V: Là thể tích.
- Sđáy: Diện tích đáy.
- h: Là chiều cao.
Một phép vị tự tỉ số k biến khối đa diện có thể tích V thành khối đa diện có thể tích V’ thì V’/V = |k|3
Tham khảo thêm:
- Công thức tính nồng độ mol, số mol chính xác 100%
- Cách giải bất phương trình từ cơ bản đến nâng cao chi tiết từ A – Z
Tỉ số thể tích hai khối chóp tam giác
Nếu A′, B′, C ′ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác SABC. Khi đó:
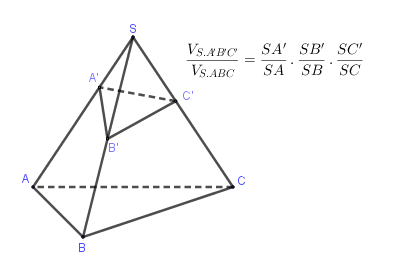
Các dạng bài tập liên quan đến thể tích khối chóp
Dạng 1: Tính thể tích khối chóp có cạnh bên vuông góc với đáy
Một hình chóp có một cạnh bên vuông góc với đáy thì cạnh bên đó chính là đường cao.
Một hình chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì cạnh bên là giao tuyến của hai mặt đó vuông góc với đáy
Ví dụ 1: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân ở B, AC=a√2, SA vuông góc với mặt phẳng (ABC), SA = a. Tính thể tích khối chóp S.ABC
Lời giải:
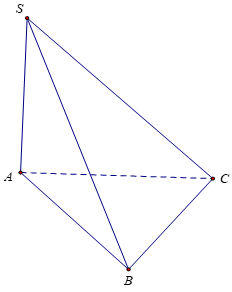
ABC là tam giác vuông cân ở B, AC=a√2 nên
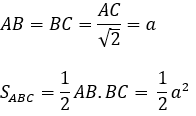
SA vuông góc với mặt phẳng ABC nên SA là đường cao
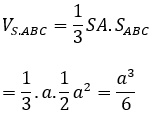
Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. SA vuông góc với mặt phẳng (ABC). Góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 30º.Tính theo a thể tích của khối chóp S.ABC
Lời giải
Do SA ⊥ (ABC) nên AB là hình chiếu vuông góc của SB lên mặt phẳng (ABC).
⇒ Góc giữa đường thẳng SB và mặt phẳng (ABC) là ![]()
Xét tam giác SAB vuông tại A có:
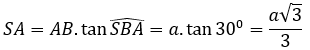
∆ABC đều cạnh a nên
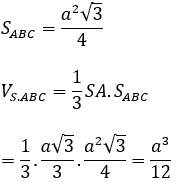
Ví dụ 3: Cho hình chóp S.ABC có cạnh bên SA vuông góc với đáy và AB = a, AC = 2a, góc BAC = 120º. Mặt phẳng (SBC) tạo với đáy một góc 60º. Tính theo a thể tích khối chóp S.ABC
Lời giải:
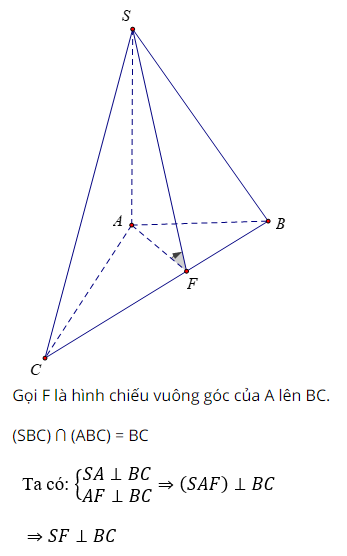
Vậy góc giữa (SBC) và (ABC) là góc SFA = 60º
Xét tam giác ABC, AB = a, AC = 2a, góc BAC = 120º có:
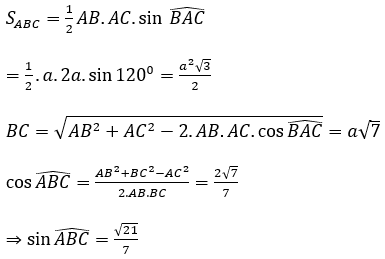

Dạng 2: Tính thể tích khối chóp đều
Ví dụ 1: Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.
Lời giải:
Giả sử khối chóp S.ABCD đều có đáy là hình vuông cạnh a tâm O và cạnh bên SD = 2a. Khi đó SO⊥ (ABCD).
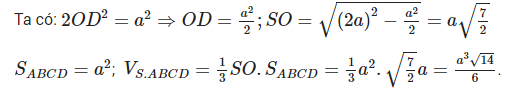
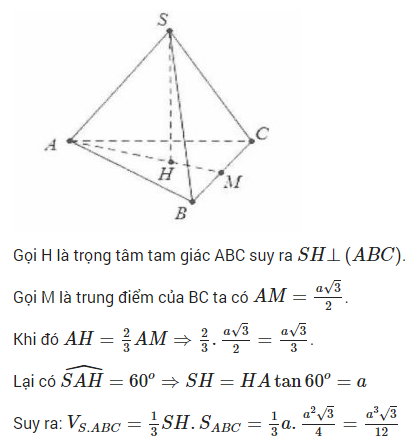
Ví dụ 2: Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a, cạnh bên tạo với đáy một góc bằng 60∘. Tính thể tích khối chóp đã cho.
Dạng 3: Tính thể tích khối chóp có mặt bên vuông góc với đáy
Để xác định đường cao hình chóp, ta vận dụng định lí sau:
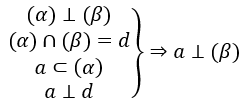
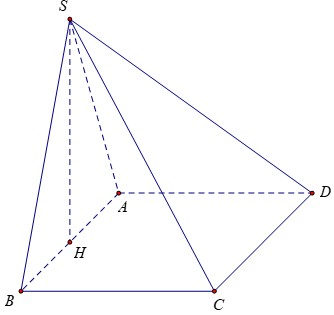
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a. Mặt bên (SAB) là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD. Tính thể tích khối S.ABCD
Lời giải:
Gọi H là trung điểm của AB
∆SAB đều nên SH ⊥ AB
(SAB) ⊥ (ABCD) ⇒ SH ⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.
Ta có: ∆SAB đều cạnh a nên SH = a√3/2
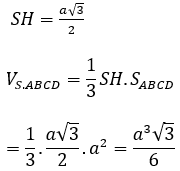
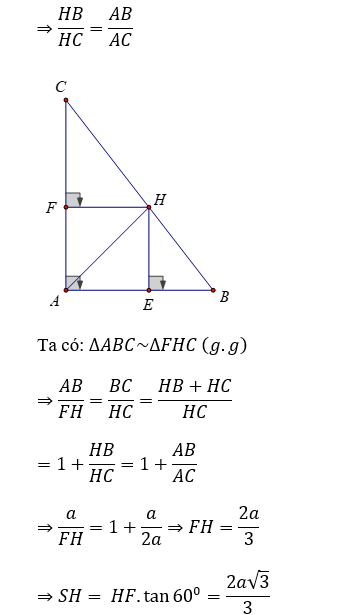
Ví dụ 2: Cho hình chóp S.ABC có đáy là tam giác vuông tại A, AB = a, AC = 2a. Mặt phẳng (SBC) vuông góc với đáy, hai mặt phẳng (SAB) và (SAC) cùng tạo với mặt phẳng đáy góc 60º. Tính thể tích của khối S.ABC theo a
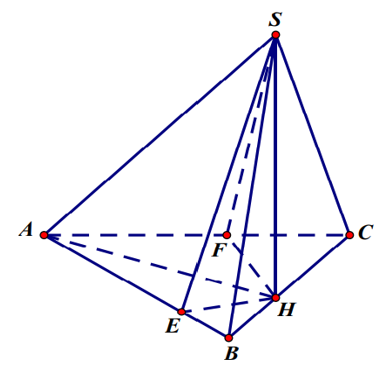
Gọi H là hình chiếu của S lên BC; E, F lần lượt là hình chiếu của H lên AB, AC.
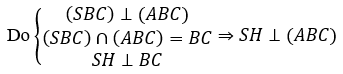
Khi đó, ta có: góc giữa (SAB) và (SAC) với mặt đáy (ABC) lần lượt là các góc ∠(SEH ) và ∠(SFH )
⇒∠(SEH)=∠(SFH) = 60º
Xét các tam giác vuông SHE và SHF có:
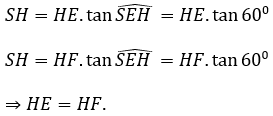
Do HE = HF nên AH là phân giác của góc BAC.
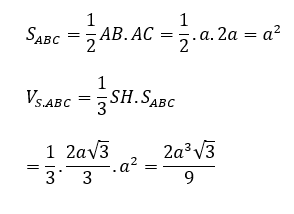
Dạng 4: Tính tỉ lệ thể tích các khối chóp.
Bước 1: Chia các khối chóp cần tính tỉ lệ thể tích thành các khối chóp tam giác tương ứng với nhau.
Bước 2: Áp dụng công thức tính tỉ số thể tích các khối chóp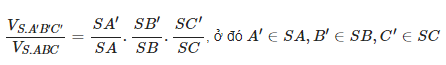
Ví dụ 1: Cho khối chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 77. Mặt phẳng (α) đi qua A cắt cạnh SC tại trung điểm N, cắt cạnh SB tại điểm M sao cho SM/SB=6/7 và cắt cạnh SD tại điểm P. Tính thể tích khối S.AMNP.
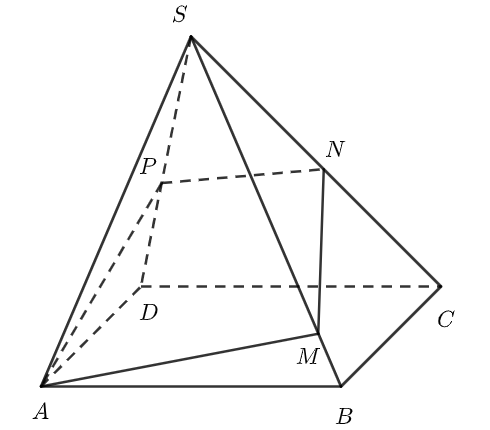
Áp dụng công thức tính nhanh với a=1, b=7/6, c=2 và d=a+c-b=1+2-7/6=11/6 ta có:
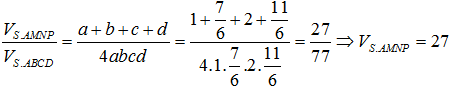
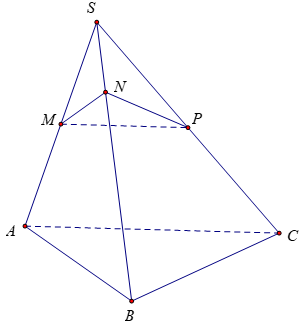
Ví dụ 2: Cho hình chóp SABC. Trên 3 cạnh SA, SB, SC lần lượt lấy 3 điểm M, N, P, sao cho SA=2SM; SB=3SN; SC=2SP. Tính ![]()
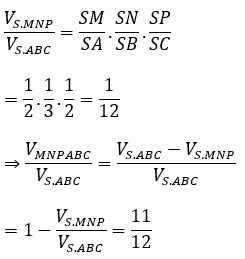
Ta có:
Hy vọng với những kiến thức về định nghĩa, tính chất và công thức tính thể tích khối chóp có thể giúp các bạn vận dụng giải các bài toán liên quan đến khối chóp nhanh chóng và đơn giản nhé