Đường tròn lượng giác là một nội dung kiến thức rất hay nhưng cũng rất phức tạp và khó. Điều này khiến học sinh bị nhầm lẫn hoặc chưa nắm bắt được kiến thức phần lượng giác
Vì thế trong bài viết dưới đây chúng tôi sẽ giúp bạn tóm tắt những nội dung chính quan trọng. Để từ đó bạn sẽ nắm bắt được phần kiến thức trong phần này nhé !
Tham khảo bài viết khác:
1. Định nghĩa về đường tròn lượng giác
– Trong toán học, đường tròn đơn vị hay vòng tròn đơn vị là đường tròn với bán kính là 1 đơn vị. Thông thường, đặc biệt là trong lượng giác, vòng tròn đơn vị là hình tròn có bán kính 1 với tâm tại gốc tọa độ (0,0) trong không gian 2 chiều. Nó thường được ký hiệu là S1.
2. Đường tròn đơn vị trong lượng giác

+) Vòng tròn lượng giác, còn được gọi là đường tròn đơn vị, có bán kính R=1, tâm trùng với gốc tọa độ.
+) Trục hoành là trục cos, trục tung là trục sin.
+) Trục tan có gốc là điểm A và vuông góc với trục cos, trục cotan có gốc là điểm B vuông góc với trục sin.
+) Chiều dương là chiều ngược chiều kim đồng hồ, chiều âm cùng chiều kim đồng hồ.
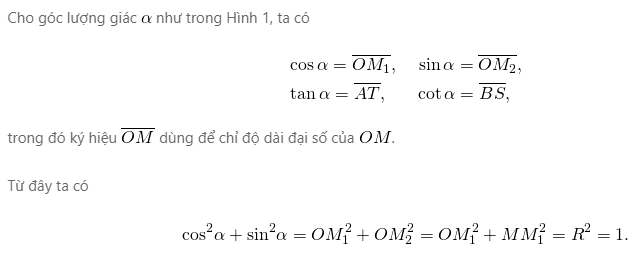
Dấu của các giá trị lượng giác
| Góc phần tư số | I | II | III | IV |
| Giá trị lượng giác | ||||
| sin x | + | + | – | – |
| cos x | + | – | – | + |
| tan x | + | – | + | – |
| cot x | + | – | + | – |
Bảng giá trị lượng giác từ 0 độ đến 180 độ
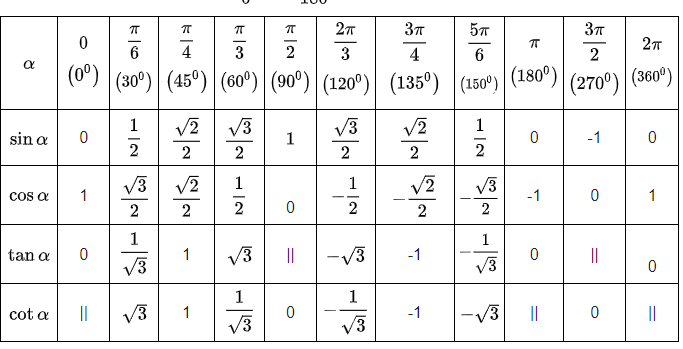
Ngoài ra, các bạn có thể tham khảo công thức lượng giác để biết cách học ghi nhớ bảng giá trị lượng giác nhé
Hướng dẫn sử dụng vòng tròn lượng giác
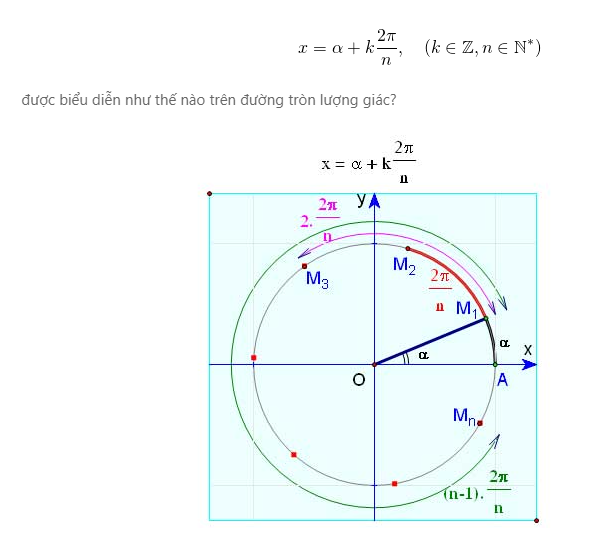
– Biểu diễn góc (cung) trên đường tròn lượng giác là một kỹ năng quan trọng trong lượng giác. Thành thạo kỹ năng này sẽ giúp người học nhiều thuận lợi trong quá trình tổng hợp nghiệm hay loại nghiệm đối với các phương trình lượng giác có điều kiện.
Ta sẽ tìm hiểu góc

Cám ơn bạn đã theo dõi bài viết này, hy vọng với những kiến thức trên sẽ giúp bạn giải quyết các bài toán nhé !