Tính chất hình bình hành, định nghĩa, dấu hiệu nhận biết từ A – Z

Ở chuyên mục Giáo Dục hôm nay, điện máy Ebest chia sẻ lý thuyết hình bình hành là gì? Tính chất hình bình hành và dấu hiệu nhận biết hình bình hành kèm theo các ví dụ có lời giải chi tiết để các bạn cùng tham khảo nhé

Hình bình hành là gì?

Hình bình hành là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song cắt nhau. Nói cách khác dễ hiểu hơn hình bình hành là tứ giác có các cạnh dối song song.

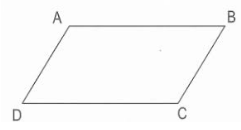
Ví dụ: tứ giác ABCD là hình bình hành khi và chỉ khi AB // CD, AD // BC

Tính chất hình bình hành

Trong một hình bình hành có:

• Các cạnh đối song song và bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Dấu hiệu nhận biết hình bình hành

• Tứ giác có hai cặp cạnh đối song song là hình bình hành.
• Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành.
• Tứ giác có một cặp cạnh đối vừa song song và vừa bằng nhau là hình bình hành.
• Tứ giác có hai góc đối bằng nhau là hình bình hành.
• Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
• Hình thang có hai cạnh đáy bằng nhau là hình bình hành.
• Hình thang có hai cạnh bên song song là hình bình hành

Tham khảo thêm:

• Công thức tính diện tích hình bình hành, chu vi hình bình hành từ A – Z
• Hình thang cân là gì? Tính chất hình thang cân, dấu hiệu nhận biết từ A – Z
• Hình thang là gì? Tính chất hình thang, cách chứng minh từ A – Z

Bài tập về hình bình hành có lời giải

Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF.

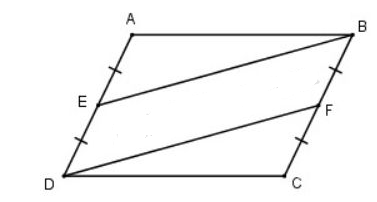
ABCD hình bình hành nên DE // BF và AD = BC

E là trung điểm của AD (giả thiết) nên DE = ½ AD (tính chất trung điểm)

F là trung điểm của BC (giả thiết) nên BF = ½ BC(tính chất trung điểm)

Mà AD = BC (chứng minh trên) nên DE = BF

Tứ giác BEDF có DE // BF và DE = BF (chứng minh trên)

⇒ Tứ giác BEDF là hình bình hành (theo dấu hiệu nhận biết hình bình hành).

⇒ BE = DF(tính chất hình bình hành).

Cách khác:

ABCD là hình bình hành ⇒ AB = CD, AD = BC, A^∧ =C^∧.

E là trung điểm của A D ⇒ AE = ½ AD (tính chất trung điểm)

F là trung điểm của BC ⇒ BF = ½ BC (tính chất trung điểm)

Mà AD = BC (chứng minh trên)

⇒ AE = CF

+ Xét ΔAEB và ΔCFD có: AB = CD, A^∧ =C^∧, AE =CF (chứng minh trên)

⇒ ΔAEB = ΔCFD (c.g.c)

⇒ EB = DF

Ví dụ 2: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF.

b) Tứ giác DEBF là hình gì ? Vì sao ?

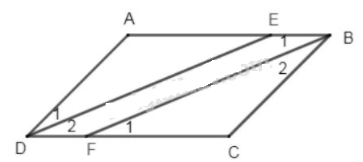
a) Vì ABCD là hình bình hành (giả thiết)

⇒ ˆABC = ^ˆADC (tính chất hình bình hành ) (1)

Vì BF là tia phân giác ˆABC (giả thiết)

⇒ ˆB₁ = ˆB₂ =ˆABC/2 (tính chất tia phân giác) (2)

Vì DE là tia phân giác ˆADC (giả thiết)

⇒ ˆD₁ =ˆ D₂ = ˆADC/2 (tính chất tia phân giác) (3)

Từ (1), (2), (3) ⇒ ˆD₂=ˆB₁(4)

Có AB // DC ( vì ABCD là hình bình hành)

Suy ra: ˆB₁ =ˆF₁ (so le trong) (5)

Từ (4) và (5) suy ra ˆF₁ =ˆD₂ mà hai góc này ở vị trí đồng vị nên DE // BF (dấu hiệu nhận biết hai đường thẳng song song)

b) ABCD là hình bình hành (giả thiết)

⇒ AB // CD (tính chất hình bình hành) hay BE // DF

Xét tứ giác DEBF có BE // DF(chứng minh trên) và DE//BF (theo câu a)

Suy ra tứ giác DEBF là hình bình hành (dấu hiệu nhận biết hình bình hành).

Ví dụ 3: Trong các tứ giác sau, tứ giác nào là hình bình hành? Vì sao?

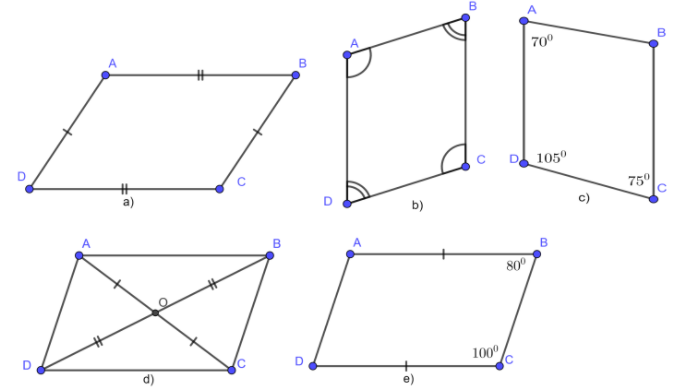
Lời giải

a) Tứ giác ABCD có AB = CD, BC = AD do đó ABCD là hình bình hành.

b) Tứ giác ABCD có A^∧ = C^∧, B^∧ = D^∧ do đó ABCD là hình bình hành.

c) Tứ giác ABCD có A^∧ + D^∧ = 70⁰ + 105⁰ = 175⁰ ≠ 180⁰ nên AB và CD không song song. Suy ra, ABCD không phải hình bình hành

d) Tứ giác ABCD có hai đường chéo là AC vad BD. AC giao BD tại O. Ta có: OA = OC, OB = OD nên ABCD là hình bình hành.

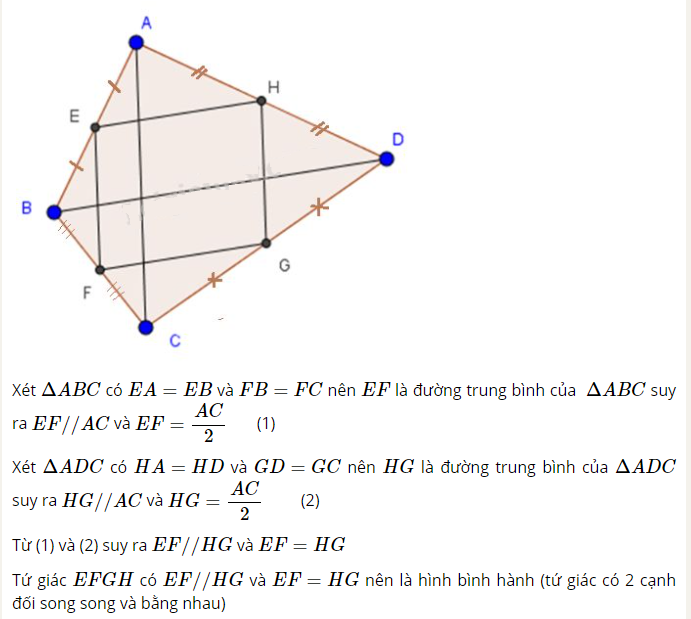
Ví dụ 4: Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC,CD, DA.Tứ giác EFGH là hình gì ? Vì sao ?

Bên trên chính là toàn bộ lý thuyết về hình bình hành là gì? Dấu hiệu nhận biết và tính chất hình bình hành có thể giúp các bạn vận dụng vào để chứng minh tứ giác là hình bình hành nhé